Рабочая зона земляного полотна: различия между версиями
Admin (обсуждение | вклад) |
Admin (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
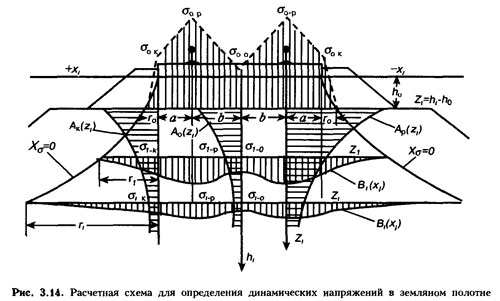
РАБОЧАЯ ЗОНА ЗЕМЛЯНОГО ПОЛОТНА — зона под рельсошпальной решеткой ж.-д. пути, в которой реализуется динамическое силовое воздействие подвижного состава. Для определения рабочей зоны земляного полотна предложена схема расчета напряжений (рис. 3.14), основанная на следующих основных допущениях. | РАБОЧАЯ ЗОНА ЗЕМЛЯНОГО ПОЛОТНА — зона под рельсошпальной решеткой ж.-д. пути, в которой реализуется динамическое силовое воздействие подвижного состава. Для определения рабочей зоны земляного полотна предложена схема расчета напряжений (рис. 3.14), основанная на следующих основных допущениях. | ||
| − | Zp 3 14.jpg | + | [[Файл:Zp 3 14.jpg]] |
| − | 1.Напряжения в земляном полотне определяются от уровня основной площадки, под которой понимается горизонтальная расчетная плоскость, проходящая через бровки земляного полотна на глубине | + | 1.Напряжения в земляном полотне определяются от уровня основной площадки, под которой понимается горизонтальная расчетная плоскость, проходящая через бровки земляного полотна на глубине ho от подошвы шпалы. Конфигурация нагрузки в виде эпюры |
| − | напряжений принимается на основе натурных измерений на эксплуатируемом пути, которые обозначаются: в подрельсовых сечениях - | + | напряжений принимается на основе натурных измерений на эксплуатируемом пути, которые обозначаются: в подрельсовых сечениях - σo-p, под концами шпалы - σo-k по оси колеи - σo-o |
2. За расчетные сечения в земляном полотне (где возникают максимальные динамические напряжения) принимаются вертикальные сечения, проходящие через рельсовые нити. В других сечениях напряжения определяются функцией распределения Bt(xj), где Xj — расстояние на любом i-ом горизонте от оси колеи до расчетного сечения j. | 2. За расчетные сечения в земляном полотне (где возникают максимальные динамические напряжения) принимаются вертикальные сечения, проходящие через рельсовые нити. В других сечениях напряжения определяются функцией распределения Bt(xj), где Xj — расстояние на любом i-ом горизонте от оси колеи до расчетного сечения j. | ||
| − | 3.Давление от подошвы шпалы на грунтовый массив из зернистого материала (балластный слой и земляное полотно) передается в поперечном сечении пути по гиперболическим поверхностям | + | 3.Давление от подошвы шпалы на грунтовый массив из зернистого материала (балластный слой и земляное полотно) передается в поперечном сечении пути по гиперболическим поверхностям Хσ = 0, за пределами которых динамические напряжения практически отсутствуют. |
| − | 4.Изменение динамических напряжений по глубине земляного полотна в различных его сечениях определяется функцией затухания напряжений Аj | + | 4.Изменение динамических напряжений по глубине земляного полотна в различных его сечениях определяется функцией затухания напряжений Аj(zi), которая описывается экспоненциальными зависимостями вида Aj(zi) = exp (-λjzi), где λj — коэффициенты затухания напряжений по глубине земляного полотна в вертикальных сечениях j от уровня основной площадки zi =hi — ho; hi — глубина от подошвы шпалы до расчетной точки. |
| − | 5.Коэффициенты затухания | + | 5.Коэффициенты затухания λj принимаются в качестве интегрального параметра, характеризующего силы внутреннего сопротивления грунта земляного полотна при динамическом воздействии подвижного состава. Приняты следующие обозначения: λр, λк и λо — коэффициенты затухания напряжений соответственно под рельсами, концами шпал и по оси колеи. Экспериментально установлено, что коэффициенты затухания увеличиваются с ростом скорости движения поездов v в линейной зависимости λj = aj + bjv. |
| − | С учетом принятых допущений и приведенной на рис. 3.14 расчетной схемы динамические напряжения в любой точке насыпи , определяются по формуле: | + | С учетом принятых допущений и приведенной на рис. 3.14 расчетной схемы динамические напряжения в любой точке насыпи , определяются по формуле: σi-j=σo-p=Ap(zi)Bi(xj). Входящие в эту формулу параметры устанавливают на основе экспериментальных и расчетно-теоретических данных. |
| − | Так, напряжения | + | Так, напряжения σo-p на основной площадке в подрельсовом сечении определяются в соответствии с существующими «Правилами»; функция затухания напряжений Ap(zi) по глубине насыпи в в подрельсовом сечении как Ap(zi)=exp(-λpzi).Функция распределения напряжений Bi(xj) в сечениях: по оси колеи (xo=0) |
| + | Bi(xo)=γo-o exp(λp-λo)zi; под рельсами (xp=b) Bi(xp)=1; под концами шпалы | ||
| + | (xк=a+b) Bi(xк)=γo-кexp(λp-λк)zi. На эксплуатируемом пути экспериментально установлены значения: | ||
| + | γo-p=1,00; γo-к=0,61; γo-o=0,33; ap=0,71; bp=0,00274; aк=0,86; bк=0,00110; ao=0,48; bo=0,00325. | ||
| + | Предложенный метод позволяет определять границы рабочей зоны по глубине и в поперечном сечении насыпи; оценить влияние скоростей движения поездов, в том числе и на скоростных магистралях; выделить отдельные зоны с повышенной динамической активностью; предложить модель напряженного состояния насыпи. | ||
| + | '''Границы рабочей зоны.''' Интенсивность затухания максимальных динамических напряжений σд по глубине характеризуется коэффициентом λр, который зависит от рассматриваемого интервала глубин Δzi, в земляном полотне, конструкции ж.-д. пути и его состояния (ровные рельсы, наличие неровностей | ||
| + | на пути) и скорости движения поездов. В наибольшей степени динамические напряжения затухают в верхнем слое земляного полотна в пределах глубин Δzi= 0-0,5 м. Например, при скорости движения поезда | ||
| + | 120 км/ч коэффициент λp в этом слое полотна в 4 раза больше, чем в интервале глубин Δzi= 0,5- 1,5 м. Наличие изолированных неровностей на пути приводит к увеличению в 2,5—3 раза ударно-динамических напряжений на основной площадке и к более резкому их затуханию по глубине земляного полотна. При скорости движения поезда 100 км/ч напряжения σд на глубинах zi = 1 м составляют 38%, при | ||
| + | zi = 2 м - 14%, а при zi = 4 м - 2% от аналогичных напряжений на основной площадке. На глубине zi = 4 м динамические напряжения практически отсутствуют, т. к. составляют всего 2% от действующих на этом же уровне постоянных статических напряжений σп, от собственного веса грунта σγ и веса верхнего строения пути σвс. В поперечном сечении насыпи балластная призма за пределами шпалы, обочина и откосы насыпи не испытывают силового нагружения от подвижного состава. Для двухпутной линии в случае совместного воздействия двух встречных поездов расчет динамических напряжений в насыпи проводится в подрельсовом сечении одного из путей без учета влияния подвижного состава, следующего по второму пути. | ||
| + | '''Влияние скоростей движения подвижного состава.''' Увеличение скоростей движения поездов приводит к росту напряжений на основной площадке земляного полотна. Однако приращение напряжений Δσ,- для одного и того же диапазона скоростей движения Δvi по мере роста скоростей движения снижается. Наибольшее приращение напряжений наблюдается в интервалах повышения скоростей движения Δv1 =20-80 км/ч, где оно составляет Δσ = 19,4%. В интервале Δvi = 140-200 км/ч наблюдаются более медленный (почти в два раза) по сравнению с интервалом Δv = 20-80 км/ч рост напряжений на основной площадке и снижение этих величин в теле насыпи на глубинах zi > 1 м. Это связано как с относительным снижением коэффициента вертикальной динамики kвд скоростного подвижного состава (например, для электропоезда ЭР-200 в 7,5 раза в интервале скоростей Δvi = 140-200 км/ч по сравнению с Δv2 = 80—140 км/ч), так и с инерционными свойствами грунтовой массы насыпи, которая не успевает реагировать на кратковременные силовые нагрузки подвижного состава. Реакция грунта на воздействия подвижного состава на разных глубинах в насыпи оценивается динамическим коэффициентом nд, представляющим собой отношение напряжений на горизонтах zj- при различных скоростях σvi- к статическим напряжениям на этом горизонте σст, т. е. nд =σvi*σст. Расчеты показали, что чем выше скорость движения, т. е. чем быстрее перемещается поездная нагрузка через данное сечение пути, тем на меньшую глубину проникает ее влияние. При скоростях движения 150-200 км/ч на основной площадке (при zi = 0) динамический коэффициент nд= 1,41-1,62; на глубине zi = 0,5 м nд=1,18- 1,19. На глубинах zi > 1,0 м nд< 1 вследствие больших сил внутреннего сопротивления грунта. | ||
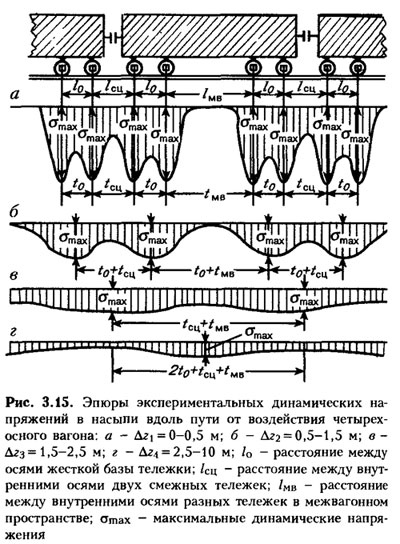
| + | '''Частота и продолжительность динамических воздействий.''' При воздействии подвижного состава насыпь работает в режиме многократного циклического упругого силового нагружения. Поэтому для оценки рабочей зоны насыпи важное значение имеет не только величина действующих напряжений, но и частота и продолжительность их воздействий, а также общее количество таких циклов. Характер изменения напряжений вдоль пути представлен в виде эпюр на рис. 3.15. | ||
| + | [[Файл:Zp_3_15.jpg]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Как следует из рисунка, интенсивность силового нагружения насыпи существенно изменяется по глубине рабочей зоны. Частота циклов «нагрузка - разгрузка» (f,Гц) определяется по формуле f=1/ti=0,278v/li, где v - скорость движения поезда, км/ч; li - расстояния между осями экипажей,м. Расчеты частот , выполненные для пассажирского вагона электропоезда ЭР-200 и четырехосного грузового вагона при различных значениях li, показали, что в наиболее сложных динамических условиях работает основная площадка и верхняя часть насыпи (Δzt = 0-0,5 м), где проявляется влияние отдельных осей вагонов. При любой скорости движения от воздействия каждого четырехосного вагона возникают три группы частот, величина которых зависит от расстояний lσ, lсц и lмв. Так, частоты силовых воздействий для пассажирского поезда при скорости 200 км/ч составляют: fI = 3,4 Гц, fII=15 Гц, fIII = 22,2 Гц, а грузового поезда из четырехосных вагонов при скорости 100 км/ч соответственно: fI = 3,3 Гц, | |
| − | Как следует из рисунка, интенсивность силового нагружения насыпи существенно изменяется по глубине рабочей зоны. Частота циклов «нагрузка - разгрузка» ( , Гц) определяется по формуле | + | fII=11,7 Гц, fIII = 15,4 Гц. Для глубин Δz2=0,5-1,5 м наблюдаются две группы частот: при скорости пассажирского поезда 200 км/ч fI = 9 Гц, fII = 3 Гц; при скорости грузового поезда 100 км/ч |
| − | = 1 | + | fI = 6,7 Гц и fII= 2,8 Гц. Для глубин Δzз= 1,5-2,5 м наибольшие частоты для скоростного |
| − | fII=11,7 Гц, fIII = 15,4 Гц. Для глубин | + | пассажирского поезда (при v = 200 км/ч) и грузового (при и = 100 км/ч) практически одинаковы и равны 2 Гц. На глубинах Δzi >2,5 м цикличность приложения силовой поездной нагрузки практически не обнаружена. Общее количество нагружений N верхней части насыпи Δzi = 0-0,5 м может быть принято равным числу осей подвижного состава ni, т. е. N1=Σn1. Для интервала глубин Δz2 = 0,5- 1,5 м, где максимум нагружений возникает только под тележками вагонов, число динамических воздействий на насыпь N2 =Σn1/2. В пределах глубин Δzз = 1,5—2,5 м максимумы напряжений возникают в средней части двух |
| − | fI = 6,7 Гц и fII= 2,8 Гц. Для глубин | + | тележек соседних вагонов, а общее количество нагружений составляет Nз =Σni/4, т.е. равно числу вагонов в поезде. На глубинах Δz1 > 2,5-3,0 м при проходе поезда появляется незначительная дополнительная нагрузка, близкая по своему воздействию к статической, которая практически равномерно распределена вдоль пути под всем поездом. Таким образом, рабочая зона по глубине насыпи неоднородна по своей реакции на воздействие подвижного состава. |
| − | пассажирского поезда (при v = 200 км/ч) и грузового (при и = 100 км/ч) практически одинаковы и равны 2 Гц. На глубинах | ||
| − | тележек соседних вагонов, а общее количество нагружений составляет Nз = | ||
| − | Динамической активностью слоев грунта насыпи D называют произведение количества циклов нагружения | + | Динамической активностью слоев грунта насыпи D называют произведение количества циклов нагружения Ni в интервале глубин Δzi на среднее значение действующих в этом же интервале динамических напряжений |
| − | + | σд, т.е. Di = Ni*σд. Результаты расчетов динамической активности рабочей зоны на скоростных участках пути со смешанным движением поездов показали, что динамическая активность грунта насыпи от воздействия грузового поезда из 60 вагонов выше, чем от воздействия пассажирских поездов ЭР-200, | |
| − | в 6-7 раз (поезд из 15 вагонов) и в 3,5-4,1 раза (поезд из 25 вагонов). По глубине насыпи динамическая активность рабочей зоны резко уменьшается для пассажирских и грузовых поездов и составляет: при | + | в 6-7 раз (поезд из 15 вагонов) и в 3,5-4,1 раза (поезд из 25 вагонов). По глубине насыпи динамическая активность рабочей зоны резко уменьшается для пассажирских и грузовых поездов и составляет: при Δz2= 0,5-l,5 м - 25-29%, при Δz3=1,5-2,5 м - 6-7% от аналогичных величин D1 в верхней части насыпи вблизи основной площадки ( Δz1 = 0-0,5 м). |
Циклическое силовое нагружение продолжается в течение времени поезда Т (в с), которое при длине поезда L (в м) и скорости движения v (в км/ч) определяется по формуле: Т = 3,6 L/v. Продолжительность динамического силового воздействия на насыпь составляет: для пассажирских поездов при скорости | Циклическое силовое нагружение продолжается в течение времени поезда Т (в с), которое при длине поезда L (в м) и скорости движения v (в км/ч) определяется по формуле: Т = 3,6 L/v. Продолжительность динамического силового воздействия на насыпь составляет: для пассажирских поездов при скорости | ||
| Строка 52: | Строка 49: | ||
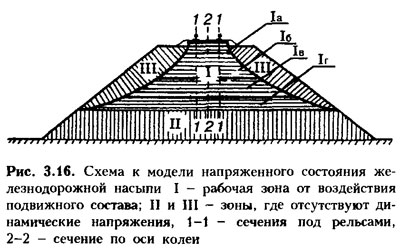
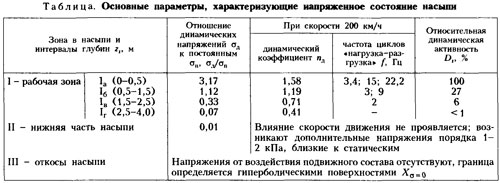
'''Модель напряженного состояния насыпи.''' Схема к модели напряженного состояния насыпи приведена на рис. 3.16, а основные параметры, характеризующие это состояние, даны в таблице. В верхней части рабочей зоны максимальные динамические напряжения возникают под рельсами (сечения 1-1), а минимальные - по оси колеи (сечение 2-2). такое распределение напряжений характерно при подбивке шпал в подрельсовых сечениях, как это регламентируют нормы содержания пути. | '''Модель напряженного состояния насыпи.''' Схема к модели напряженного состояния насыпи приведена на рис. 3.16, а основные параметры, характеризующие это состояние, даны в таблице. В верхней части рабочей зоны максимальные динамические напряжения возникают под рельсами (сечения 1-1), а минимальные - по оси колеи (сечение 2-2). такое распределение напряжений характерно при подбивке шпал в подрельсовых сечениях, как это регламентируют нормы содержания пути. | ||
| + | |||
| + | [[Файл:Zp_3_16.jpg]] | ||
| + | |||
| + | [[Файл:Zp_table_5.jpg]] | ||
Воздействие подвижного состава по глубине насыпи имеет специфические особенности, которые позволяют разделить рабочую зону I на характерные четыре части Iа, Iб, Iв, Iг, различающиеся между собой по величине и виду действующих напряжений; по частоте повторения динамических напряжений и общему количеству циклов "нагрузки - разгрузки" грунта; по влиянию скоростей движения поездов; по динамической активности (реакции) отдельных слоев грунта насыпи на воздействия подвижного состава. | Воздействие подвижного состава по глубине насыпи имеет специфические особенности, которые позволяют разделить рабочую зону I на характерные четыре части Iа, Iб, Iв, Iг, различающиеся между собой по величине и виду действующих напряжений; по частоте повторения динамических напряжений и общему количеству циклов "нагрузки - разгрузки" грунта; по влиянию скоростей движения поездов; по динамической активности (реакции) отдельных слоев грунта насыпи на воздействия подвижного состава. | ||
| − | В нижней части рабочей зоны ( | + | В нижней части рабочей зоны ( Δzi = 2,5-4,0 м) воздействие подвижного состава можно рассматривать как дополнительную статическую нагрузку, величина которой составляет порядка 1% от постоянно действующей на этом уровне статической нагрузки σп. В зоне II, находящейся на глубине z>4 м, динамика подвижного состава не проявляется; здесь действуют только постоянные напряжения от веса вышележащего грунта. В откосах насыпи (зона III) динамические напряжения от силового воздействия подвижного состава практически отсутствуют и положение этой зоны определяется гиперболическими поверхностями Xσ=0. |
Предложенное понятие "рабочая зона" и определение ее динамической структуры позволяют по-новому подходить к оценке влияния воздействия подвижного состава на земляное полотно (насыпи), в том числе на скоростных магистралях; совершенствовать расчеты земляного полотна по определению требуемой плотности грунта, осадок оснований насыпей и основных площадок выемок, а также дает возможность рассчитывать динамические нагрузки на различные инженерные сооружения и устройства (водопроводные трубы в насыпях, защитные слои из синтетических материалов, поддерживающие сооружения, и т.п.). | Предложенное понятие "рабочая зона" и определение ее динамической структуры позволяют по-новому подходить к оценке влияния воздействия подвижного состава на земляное полотно (насыпи), в том числе на скоростных магистралях; совершенствовать расчеты земляного полотна по определению требуемой плотности грунта, осадок оснований насыпей и основных площадок выемок, а также дает возможность рассчитывать динамические нагрузки на различные инженерные сооружения и устройства (водопроводные трубы в насыпях, защитные слои из синтетических материалов, поддерживающие сооружения, и т.п.). | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
[[Категория:Земляное полотно]] | [[Категория:Земляное полотно]] | ||
Версия 18:43, 10 сентября 2017
РАБОЧАЯ ЗОНА ЗЕМЛЯНОГО ПОЛОТНА — зона под рельсошпальной решеткой ж.-д. пути, в которой реализуется динамическое силовое воздействие подвижного состава. Для определения рабочей зоны земляного полотна предложена схема расчета напряжений (рис. 3.14), основанная на следующих основных допущениях.
1.Напряжения в земляном полотне определяются от уровня основной площадки, под которой понимается горизонтальная расчетная плоскость, проходящая через бровки земляного полотна на глубине ho от подошвы шпалы. Конфигурация нагрузки в виде эпюры напряжений принимается на основе натурных измерений на эксплуатируемом пути, которые обозначаются: в подрельсовых сечениях - σo-p, под концами шпалы - σo-k по оси колеи - σo-o
2. За расчетные сечения в земляном полотне (где возникают максимальные динамические напряжения) принимаются вертикальные сечения, проходящие через рельсовые нити. В других сечениях напряжения определяются функцией распределения Bt(xj), где Xj — расстояние на любом i-ом горизонте от оси колеи до расчетного сечения j.
3.Давление от подошвы шпалы на грунтовый массив из зернистого материала (балластный слой и земляное полотно) передается в поперечном сечении пути по гиперболическим поверхностям Хσ = 0, за пределами которых динамические напряжения практически отсутствуют.
4.Изменение динамических напряжений по глубине земляного полотна в различных его сечениях определяется функцией затухания напряжений Аj(zi), которая описывается экспоненциальными зависимостями вида Aj(zi) = exp (-λjzi), где λj — коэффициенты затухания напряжений по глубине земляного полотна в вертикальных сечениях j от уровня основной площадки zi =hi — ho; hi — глубина от подошвы шпалы до расчетной точки.
5.Коэффициенты затухания λj принимаются в качестве интегрального параметра, характеризующего силы внутреннего сопротивления грунта земляного полотна при динамическом воздействии подвижного состава. Приняты следующие обозначения: λр, λк и λо — коэффициенты затухания напряжений соответственно под рельсами, концами шпал и по оси колеи. Экспериментально установлено, что коэффициенты затухания увеличиваются с ростом скорости движения поездов v в линейной зависимости λj = aj + bjv.
С учетом принятых допущений и приведенной на рис. 3.14 расчетной схемы динамические напряжения в любой точке насыпи , определяются по формуле: σi-j=σo-p=Ap(zi)Bi(xj). Входящие в эту формулу параметры устанавливают на основе экспериментальных и расчетно-теоретических данных.
Так, напряжения σo-p на основной площадке в подрельсовом сечении определяются в соответствии с существующими «Правилами»; функция затухания напряжений Ap(zi) по глубине насыпи в в подрельсовом сечении как Ap(zi)=exp(-λpzi).Функция распределения напряжений Bi(xj) в сечениях: по оси колеи (xo=0) Bi(xo)=γo-o exp(λp-λo)zi; под рельсами (xp=b) Bi(xp)=1; под концами шпалы (xк=a+b) Bi(xк)=γo-кexp(λp-λк)zi. На эксплуатируемом пути экспериментально установлены значения: γo-p=1,00; γo-к=0,61; γo-o=0,33; ap=0,71; bp=0,00274; aк=0,86; bк=0,00110; ao=0,48; bo=0,00325.
Предложенный метод позволяет определять границы рабочей зоны по глубине и в поперечном сечении насыпи; оценить влияние скоростей движения поездов, в том числе и на скоростных магистралях; выделить отдельные зоны с повышенной динамической активностью; предложить модель напряженного состояния насыпи.
Границы рабочей зоны. Интенсивность затухания максимальных динамических напряжений σд по глубине характеризуется коэффициентом λр, который зависит от рассматриваемого интервала глубин Δzi, в земляном полотне, конструкции ж.-д. пути и его состояния (ровные рельсы, наличие неровностей на пути) и скорости движения поездов. В наибольшей степени динамические напряжения затухают в верхнем слое земляного полотна в пределах глубин Δzi= 0-0,5 м. Например, при скорости движения поезда 120 км/ч коэффициент λp в этом слое полотна в 4 раза больше, чем в интервале глубин Δzi= 0,5- 1,5 м. Наличие изолированных неровностей на пути приводит к увеличению в 2,5—3 раза ударно-динамических напряжений на основной площадке и к более резкому их затуханию по глубине земляного полотна. При скорости движения поезда 100 км/ч напряжения σд на глубинах zi = 1 м составляют 38%, при zi = 2 м - 14%, а при zi = 4 м - 2% от аналогичных напряжений на основной площадке. На глубине zi = 4 м динамические напряжения практически отсутствуют, т. к. составляют всего 2% от действующих на этом же уровне постоянных статических напряжений σп, от собственного веса грунта σγ и веса верхнего строения пути σвс. В поперечном сечении насыпи балластная призма за пределами шпалы, обочина и откосы насыпи не испытывают силового нагружения от подвижного состава. Для двухпутной линии в случае совместного воздействия двух встречных поездов расчет динамических напряжений в насыпи проводится в подрельсовом сечении одного из путей без учета влияния подвижного состава, следующего по второму пути.
Влияние скоростей движения подвижного состава. Увеличение скоростей движения поездов приводит к росту напряжений на основной площадке земляного полотна. Однако приращение напряжений Δσ,- для одного и того же диапазона скоростей движения Δvi по мере роста скоростей движения снижается. Наибольшее приращение напряжений наблюдается в интервалах повышения скоростей движения Δv1 =20-80 км/ч, где оно составляет Δσ = 19,4%. В интервале Δvi = 140-200 км/ч наблюдаются более медленный (почти в два раза) по сравнению с интервалом Δv = 20-80 км/ч рост напряжений на основной площадке и снижение этих величин в теле насыпи на глубинах zi > 1 м. Это связано как с относительным снижением коэффициента вертикальной динамики kвд скоростного подвижного состава (например, для электропоезда ЭР-200 в 7,5 раза в интервале скоростей Δvi = 140-200 км/ч по сравнению с Δv2 = 80—140 км/ч), так и с инерционными свойствами грунтовой массы насыпи, которая не успевает реагировать на кратковременные силовые нагрузки подвижного состава. Реакция грунта на воздействия подвижного состава на разных глубинах в насыпи оценивается динамическим коэффициентом nд, представляющим собой отношение напряжений на горизонтах zj- при различных скоростях σvi- к статическим напряжениям на этом горизонте σст, т. е. nд =σvi*σст. Расчеты показали, что чем выше скорость движения, т. е. чем быстрее перемещается поездная нагрузка через данное сечение пути, тем на меньшую глубину проникает ее влияние. При скоростях движения 150-200 км/ч на основной площадке (при zi = 0) динамический коэффициент nд= 1,41-1,62; на глубине zi = 0,5 м nд=1,18- 1,19. На глубинах zi > 1,0 м nд< 1 вследствие больших сил внутреннего сопротивления грунта.
Частота и продолжительность динамических воздействий. При воздействии подвижного состава насыпь работает в режиме многократного циклического упругого силового нагружения. Поэтому для оценки рабочей зоны насыпи важное значение имеет не только величина действующих напряжений, но и частота и продолжительность их воздействий, а также общее количество таких циклов. Характер изменения напряжений вдоль пути представлен в виде эпюр на рис. 3.15.
Как следует из рисунка, интенсивность силового нагружения насыпи существенно изменяется по глубине рабочей зоны. Частота циклов «нагрузка - разгрузка» (f,Гц) определяется по формуле f=1/ti=0,278v/li, где v - скорость движения поезда, км/ч; li - расстояния между осями экипажей,м. Расчеты частот , выполненные для пассажирского вагона электропоезда ЭР-200 и четырехосного грузового вагона при различных значениях li, показали, что в наиболее сложных динамических условиях работает основная площадка и верхняя часть насыпи (Δzt = 0-0,5 м), где проявляется влияние отдельных осей вагонов. При любой скорости движения от воздействия каждого четырехосного вагона возникают три группы частот, величина которых зависит от расстояний lσ, lсц и lмв. Так, частоты силовых воздействий для пассажирского поезда при скорости 200 км/ч составляют: fI = 3,4 Гц, fII=15 Гц, fIII = 22,2 Гц, а грузового поезда из четырехосных вагонов при скорости 100 км/ч соответственно: fI = 3,3 Гц,
fII=11,7 Гц, fIII = 15,4 Гц. Для глубин Δz2=0,5-1,5 м наблюдаются две группы частот: при скорости пассажирского поезда 200 км/ч fI = 9 Гц, fII = 3 Гц; при скорости грузового поезда 100 км/ч
fI = 6,7 Гц и fII= 2,8 Гц. Для глубин Δzз= 1,5-2,5 м наибольшие частоты для скоростного
пассажирского поезда (при v = 200 км/ч) и грузового (при и = 100 км/ч) практически одинаковы и равны 2 Гц. На глубинах Δzi >2,5 м цикличность приложения силовой поездной нагрузки практически не обнаружена. Общее количество нагружений N верхней части насыпи Δzi = 0-0,5 м может быть принято равным числу осей подвижного состава ni, т. е. N1=Σn1. Для интервала глубин Δz2 = 0,5- 1,5 м, где максимум нагружений возникает только под тележками вагонов, число динамических воздействий на насыпь N2 =Σn1/2. В пределах глубин Δzз = 1,5—2,5 м максимумы напряжений возникают в средней части двух
тележек соседних вагонов, а общее количество нагружений составляет Nз =Σni/4, т.е. равно числу вагонов в поезде. На глубинах Δz1 > 2,5-3,0 м при проходе поезда появляется незначительная дополнительная нагрузка, близкая по своему воздействию к статической, которая практически равномерно распределена вдоль пути под всем поездом. Таким образом, рабочая зона по глубине насыпи неоднородна по своей реакции на воздействие подвижного состава.
Динамической активностью слоев грунта насыпи D называют произведение количества циклов нагружения Ni в интервале глубин Δzi на среднее значение действующих в этом же интервале динамических напряжений σд, т.е. Di = Ni*σд. Результаты расчетов динамической активности рабочей зоны на скоростных участках пути со смешанным движением поездов показали, что динамическая активность грунта насыпи от воздействия грузового поезда из 60 вагонов выше, чем от воздействия пассажирских поездов ЭР-200, в 6-7 раз (поезд из 15 вагонов) и в 3,5-4,1 раза (поезд из 25 вагонов). По глубине насыпи динамическая активность рабочей зоны резко уменьшается для пассажирских и грузовых поездов и составляет: при Δz2= 0,5-l,5 м - 25-29%, при Δz3=1,5-2,5 м - 6-7% от аналогичных величин D1 в верхней части насыпи вблизи основной площадки ( Δz1 = 0-0,5 м).
Циклическое силовое нагружение продолжается в течение времени поезда Т (в с), которое при длине поезда L (в м) и скорости движения v (в км/ч) определяется по формуле: Т = 3,6 L/v. Продолжительность динамического силового воздействия на насыпь составляет: для пассажирских поездов при скорости 200 км/ч порядка 7-11 с; для грузового поезда при скорости 100 км/ч - 31 с. Следовательно, насыпь находится в динамическом состоянии от воздействия грузового поезда в 3—4 раза дольше, чем от воздействия скоростных пассажирских поездов. При этом динамическая активность насыпи при проходе грузового поезда значительно выше.
Модель напряженного состояния насыпи. Схема к модели напряженного состояния насыпи приведена на рис. 3.16, а основные параметры, характеризующие это состояние, даны в таблице. В верхней части рабочей зоны максимальные динамические напряжения возникают под рельсами (сечения 1-1), а минимальные - по оси колеи (сечение 2-2). такое распределение напряжений характерно при подбивке шпал в подрельсовых сечениях, как это регламентируют нормы содержания пути.
Воздействие подвижного состава по глубине насыпи имеет специфические особенности, которые позволяют разделить рабочую зону I на характерные четыре части Iа, Iб, Iв, Iг, различающиеся между собой по величине и виду действующих напряжений; по частоте повторения динамических напряжений и общему количеству циклов "нагрузки - разгрузки" грунта; по влиянию скоростей движения поездов; по динамической активности (реакции) отдельных слоев грунта насыпи на воздействия подвижного состава. В нижней части рабочей зоны ( Δzi = 2,5-4,0 м) воздействие подвижного состава можно рассматривать как дополнительную статическую нагрузку, величина которой составляет порядка 1% от постоянно действующей на этом уровне статической нагрузки σп. В зоне II, находящейся на глубине z>4 м, динамика подвижного состава не проявляется; здесь действуют только постоянные напряжения от веса вышележащего грунта. В откосах насыпи (зона III) динамические напряжения от силового воздействия подвижного состава практически отсутствуют и положение этой зоны определяется гиперболическими поверхностями Xσ=0.
Предложенное понятие "рабочая зона" и определение ее динамической структуры позволяют по-новому подходить к оценке влияния воздействия подвижного состава на земляное полотно (насыпи), в том числе на скоростных магистралях; совершенствовать расчеты земляного полотна по определению требуемой плотности грунта, осадок оснований насыпей и основных площадок выемок, а также дает возможность рассчитывать динамические нагрузки на различные инженерные сооружения и устройства (водопроводные трубы в насыпях, защитные слои из синтетических материалов, поддерживающие сооружения, и т.п.).